시간복잡도

코딩테스트를 준비하면서 프로그래머스 코딩테스트 문제풀이 전략를 읽고 테스트에 중요한 개념인 시간복잡도에 대해 정리한 글입니다.

시간복잡도란?

시간복잡도는 알고리즘이 수행되는 데 걸리는 시간과 입력 데이터의 크기(n) 사이의 관계를 나타내는 개념이다.
이는 알고리즘의 효율성을 판단하고, 더 많은 데이터가 주어졌을 때 프로그램이 얼마나 오래 걸릴지 예측하는 데 중요하다.

빅오 표기법(Big O Notation)

빅오 표기법은 최악의 경우에 대한 알고리즘의 성능을 나타내는 방법이다.

private int search(int[] array, int target) {
    for (int i = 0; i < array.length; i++) {
        if (array[i] == target) {
            return i;
        }
    }
    return -1;
}

위 코드는 평균적으로 배열 중간쯤에서 원소를 찾게 될 것이다. 하지만 최악의 경우에는 모든 원소를 순회한 후 원소를 찾게 된다.
즉 전체 배열을 순회하므로 O(N)의 시간 복잡도를 갖게 된다.

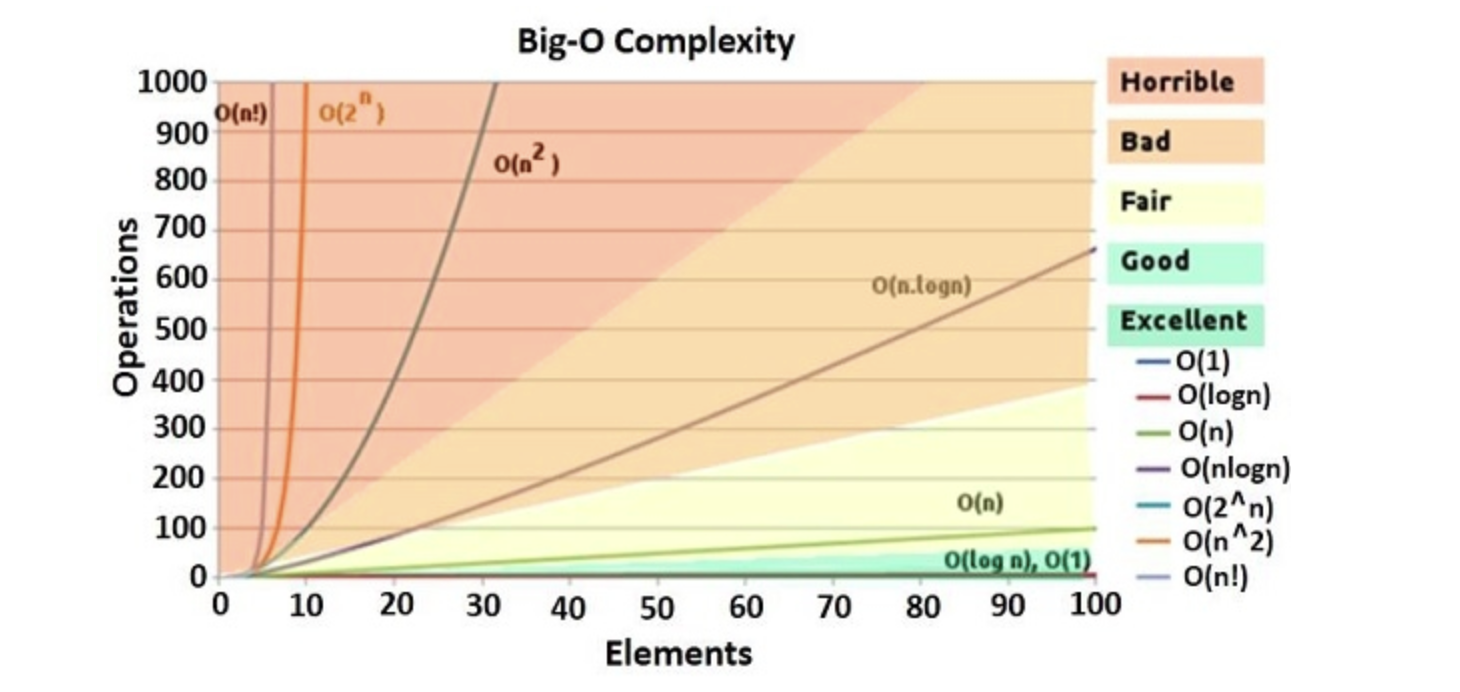
주로 사용하는 표기법은 다음과 같다:

• O(1): 상수 시간 - 데이터 크기에 상관없이 일정한 시간에 실행되는 알고리즘
• O(log n): 로그 시간 - 데이터 크기가 커질 때 로그 기반으로 증가하는 알고리즘
• O(n): 선형 시간 - 데이터 크기에 비례하여 시간이 걸리는 알고리즘
• O(n log n): 로그 선형 시간 - 정렬 알고리즘에서 흔히 나타나는 시간 복잡도
• O(n^2), O(n^3) 등: 다항 시간 - 중첩 루프와 같이 데이터 크기에 제곱 또는 세제곱 비례
• O(2^n): 지수 시간 - 입력이 커질수록 급격히 증가하는 시간 복잡도로, 피해야 할 복잡도

프로그램 실행 시간 1초라는 제한이 있을 때, 어느 정도 시간복잡도이여야 시간 제한을 만족할 수 있을까?
최악의 상황 이라고 가정할 때, 1억이 넘지 않는다면 실행 시간이 1초보다 빠른 충분히 효율적인 코드이다.

private int search(int[][] array, int target) {
    for (int i = 0; i < array.length; i++) {
        for (int j = 0 j < array[i].length; j++) {
            if (array[i][j] == target) {
                return i + j;
            }   
        }
    }
    return -1;
}

array 의 크기가 최대 N이고, array[]의 크기가 최대 M이라면, 위 코드의 시간 복잡도는 O(NM)이다.
N이 10,000 M이 100,000 일 경우 NM 은 10억이으로, 효율적이지 않은 코드이다.

시간복잡도는 코드를 작성하기 전 자신의 풀이가 충분히 효율적인지 판단할 수 있는 굉장히 중요한 요소이다.
시간복잡도를 생각하지 않고 코드를 작성하다 시간초과를 띄우게 되면 처음부터 다른 풀이를 다시 생각해야 하므로 시간적 손해가 매우 크다.